Cite this problem as Problem 45.

Background

One of the central results in computational complexity theory is the equality IP=PSPACE ([1,2]). This shows that there are protocols (called interactive proofs) where a polynomial-time classical verifier interacting with an all-powerful prover can check the answers to any PSPACE problem (i.e. problems that can be solved using exponential time and polynomial space).

In particular, since BQP, the complexity class of problems solvable by quantum computers in polynomial time, is contained in PSPACE, there is an efficient interactive proof for quantum computations. In other words, a classical verifier can be convinced of an answer to a quantum computation by interacting with a prover.

Unfortunately the interactive proof of [1,2] is not something that can be implemented in the real world: to compute a convincing proof, the prover needs to solve PSPACE-complete problems, which are (believed to be) much more difficult than BQP problems.

Thus the protocols given by the famous results of [1,2] do not give a feasible means of certifying quantum computers in the real world.

Question: Is there an interactive proof for polynomial-time quantum computations where the prover only needs the power to solve BQP problems in order to compute a convincing proof?

More formally, for every language is there an interactive protocol between a classical polynomial-time verifier and an untrusted prover where the protocol satisfies:

• Completeness: if 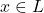, then there is a polynomial-time quantum prover 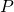that can convince 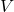that 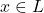with high probability.
• Soundness: if 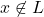, then for all provers 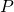(even computationally unbounded ones) the verifier 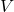will reject with high probability after interacting with .

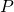Such a protocol is called a QPIP protocol for .

Partial results

There are many results on interactive proofs for quantum computations that answer different variants of the posed question. Here are a selected sample of such results:

1. Aharonov, Ben-Or, Eban, Mahadev [3] present a QPIP protocol for BQP languages where the verifier is almost entirely classical except it has the ability to store and transmit a constant number of qubits.
2. Broadbent, Fitzsimons, Kashefi [4] present a QPIP protocol for BQP languages (again with a mostly-classical verifier) that is additionally blind (meaning that the prover has no information about the quantum computation being verified).
3. Reichardt, Unger, Vazirani [5] present interactive proofs for verifying quantum computations where the verifier is entirely classical, but it instead interacts with two provers that cannot communicate but share entanglement.
4. Mahadev [6] presented a QPIP protocol with an entirely classical verifier, where the soundness condition holds under some cryptographic assumptions: the prover 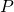are assumed to be computationally bounded, and in particular are unable to efficiently break certain problems such as the Learning-With-Errors (LWE) problem.

Each of these results use very different techniques. The last result due to Mahadev is notable for its incorporation of cryptographic assumptions. The primary goal of this Open Problem is to find a QPIP protocol where the soundness holds against all provers, not just computationally-bounded ones.

References

1. Lund, Carsten, et al. “Algebraic methods for interactive proof systems.” Journal of the ACM (JACM) 39.4 (1992): 859-868.
2. Shamir, Adi. “IP = PSPACE.” Journal of the ACM (JACM) 39.4 (1992): 869-877.
3. Aharonov, Dorit, et al. “Interactive proofs for quantum computations.” arXiv preprint arXiv:1704.04487 (2017).
4. Broadbent, Anne, Joseph Fitzsimons, and Elham Kashefi. “Universal blind quantum computation.” 2009 fiftieth Annual IEEE Symposium on Foundations of Computer Science. IEEE, (2009).
5. Reichardt, Ben W., Falk Unger, and Umesh Vazirani. “Classical command of quantum systems.” Nature 496.7446 (2013): 456-460.
6. Mahadev, Urmila. “Classical verification of quantum computations.” 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS). IEEE. (2018).