Secret key from all entangled states – Open Quantum Problems

Cite this problem as Problem 24.

Problem

Can all bipartite entangled states be used to generate secret keys?

Background

Given three parties Alice, Bob, and Eve, initially holding quantum systems $A,B,E,$ a local operation on Alice’s side is a quantum channel $\Lambda_{A\to A'}$ , i.e. a completely positive trace preserving map $\Lambda_{A\to A'} : \mathcal{T}(\mathcal{H}_A) \to \mathcal{T}(\mathcal{H}_{A'})$ . Analogously, one can define a local operation on Bob’s side. A public communication step is the process of transmitting a classical register from Alice to Bob and Eve, or from Bob to Alice and Eve. This can be modelled by the state-to-state transformation

$\displaystyle \sum_x p(x)\, |x\rangle\! \langle x|_{X} \otimes \rho_{ABE}^x \longmapsto \sum_x p(x)\, \rho_{ABE}^x \otimes |x\rangle\! \langle x|_{Y} \otimes |x\rangle\! \langle x|_{Z} ,$

where $X,Y,Z$ are registers held by Alice, Bob, and Eve, respectively. In other words, Eve, who represents the eavesdropper, can always overhear what Alice is communicating to Bob, or vice versa.

Secret key is distilled from quantum states by carrying out (finitely many) rounds of local operations and public communication. The resulting procedures are usually called LOPC protocols. We will write $\Lambda\in \mathrm{LOPC}(A:B|E \to A':B'|E')$ when we want to stress which systems at the input/output belong to Alice, Bob, and Eve.

Given a very large number $n$ of copies of some tripartite state $\rho_{ABE}$ , we can ask how much secret key Alice and Bob can generate out of it using LOPC protocols only. Specifically, they will apply an operation $\Lambda_n \in \mathrm{LOPC}\big(A^n:B^n|E^n \to K_n:K'_n|E'_n\big)$ to the initial state $\rho_{ABE}^{\otimes n}$ , where $A^n$ denotes the system made of $n$ copies of $A$ , and analogously for $B$ . The aim, at the end of the protocol, is to have Alice and Bob share a perfect secret key on some classical registers $K_n$ and $K_n'$ made of $[Rn]$ bits each (square brackets indicate the integer part). Here, $R$ represents the rate of key generation. In order for the protocol to be deemed successful, the final state should be

$\displaystyle \Lambda_n\big(\rho_{ABE}^{\otimes n}\big) \approx \left(2^{-[Rn]} \sum_{x=0}^{2^{[Rn]}-1} |x\rangle\!\langle x|_{K_n} \otimes |x\rangle\!\langle x|_{K'_n}\right) \otimes \sigma_{E'_n}\, ;$

that is, Alice and Bob should hold $[Rn]$ perfectly correlated bits, constituting their secret key, while Eve should only hold a state that is uncorrelated with Alice’s and Bob’s keys.

Partial Results

In [1] it is shown that some bound entangled states do allow the extraction of a secret key. This is an extreme counterexample to the idea that secret key is best generated from an entangled state by first distilling pure singlets, and using these to get the key. In principle, this provides a new distinction among bipartite states in those which allow key generation and those which do not. The problem asks whether this is really a new distinction.
[2] provides a one-way distillation protocol being able to distill secret key and EPR-Pairs.
In [3] a class of bound entangled states with positive key rates is provided. The smallest state of this kind is 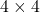$4\times 4$ , which shows that peculiar security contained in bound entangled states does not need high dimensional systems. For distilling key the Devatak-Winter protocol [2] is used.
In [4] a protocol is presented which enables two parties to extract from untrusted states an arbitrarily long and secure key, even though the amount of distillable entanglement of the untrusted states can be arbitrarily small.

References

[1] K. Horodecki, M. Horodecki, P. Horodecki, and J. Oppenheim, Secure key from bound entanglement, Phys. Rev. Lett. 94, 160502 (2005) and arXiv:quant-ph/0309110 (2003).

[2] I. Devetak and A. Winter, Distillation of secret key and entanglement from quantum states, Proc. R. Soc. Lond. A 461, 207-235 (2005) and arXiv:quant-ph/0306078 (2003).

[3] K. Horodecki, L. Pankowski, M. Horodecki, P. Horodecki, Low-dimensional bound entanglement with one-way distillable cryptographic key, IEEE Trans. Inf. Theory 54, 2621 (2008) and arXiv:quant-ph/0506203 (2005).

[4] K. Horodecki, D. Leung, H.-K. Lo, and J. Oppenheim, Quantum key distribution based on arbitrarily weak distillable entangled states, Phys. Rev. Lett. 96, 070501 (2006) and arXiv:quant-ph/0510067 (2005).