Reversible entanglement manipulation – Open Quantum Problems

Cite this problem as Problem 20.

Problem

Are PPT operations sufficient to ensure asymptotically reversibly interconversion of all, i.e. pure and mixed, bipartite entangled states?

What is the smallest non-trivial class of operations that permits asymptotically reversible interconversion of all, i.e. pure and mixed, bipartite entangled states?

Background

The concept of entanglement as a resource for quantum information processes motivates the study of its transformation properties under restricted classes of allowed operations, such as local operations and classical communication (LOCC). The key questions in such a resource theory are

Does a given state contain the resource, i.e. is it entangled?
What is the set of states we can transform a given state into under the restricted set of operations, e.g. LOCC?

A similar resource theory is given by the second law of thermodynamics where we know that one equilibrium state can be transformed adiabatically into another one if and only if the entropy increases in the process.

It is known that for a finite number of identically prepared quantum system, entanglement under LOCC is in general irreversible for both pure and mixed states. However, in the case of infinitely many identical copies of a pure state bipartite entanglement can be interconverted reversibly [1]. Specifically, defining the asymptotic transformation rate as

$\displaystyle r_{\rm LOCC} (\rho_{AB} \to \sigma_{A'B'}) := \sup \left\{ r \,\left|\; \lim_{n \to \infty} \inf_{\Lambda_n \in \rm LOCC} \left\| \Lambda_n\left(\rho_{AB}^{\otimes n}\right) - \sigma_{A'B'}^{\otimes \floor{rn}} \right\|_1 = 0 \right.\right\},$

for any two bipartite pure states $\psi_{AB}, \phi_{A'B'}$ it holds that

$\displaystyle r_{\rm LOCC} (\psi \to \phi) = r_{\rm LOCC} (\phi \to \psi)^{-1} = \frac{E_R(\psi)}{E_R(\phi)},$

where $E_R$ denotes the (relative) entropy of entanglement. This identifies $E_R$ as the unique entanglement measure in the asymptotic regime, serving as a counterpart to the thermodynamic entropy. The question then is whether a similar reversibility holds true for mixed states. This can be alternatively phrased in terms of the distillable entanglement $E_{d,\rm LOCC}(\rho) := r_{\rm LOCC} (\rho \to \Phi^+)$ and entanglement cost $E_{c,\rm LOCC}(\rho) := r_{\rm LOCC} (\Phi^+ \to \rho)^{-1}$ , where $\Phi^+$ is a two-qubit maximally entangled state. Reversibility is then equivalent to the question of whether $E_{d,\rm LOCC}(\rho) = E_{c,\rm LOCC}(\rho)$ for every bipartite state $\rho$ .

It was quickly realized that this asymptotic reversibility under LOCC operations is lost for general mixed states [2,3]. However, there are more general sets of operations for which entanglement manipulation might become reversible again. One such example is the set of positive partial transpose operations (PPT operations) [4], which are all those completely positive maps $\Lambda$ such that $\mathrm{id} \otimes \Lambda(\sigma_{AA'BB'})$ remains PPT for every PPT state $\sigma_{AA'BB'}$ . Such operations can make some mixed states, such as the totally anti-symmetric Werner state $\rho_\alpha$ , reversibly convertible, in the sense that $E_{d,\rm PPT}(\rho_\alpha) = E_{c,\rm PPT}(\rho_\alpha)$ despite the fact that $E_{d,\rm LOCC}(\rho_\alpha) < E_{c,\rm LOCC}(\rho_\alpha)$ [5].

Asymptotic reversibility for all mixed states under such a class of operations would lead to a unique entanglement measure and impose a unique ordering on entangled states, thereby playing a role similar to entropy in thermodynamics. Is entanglement theory reversible under PPT operations? If not, what is the smallest set of “free” operations that make the theory reversible?

Partial results

In [6] it was shown that multipartite entangled pure states are not reversibly interconvertible under PPT operations.
In [7], irreversibility was shown to persist under PPT operations in the bipartite setting, answering the first part of this problem in the negative. The work exhibits a class of two-qutrit states supported on the antisymmetric subspace for which 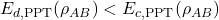$E_{d,\rm PPT}(\rho_{AB}) < E_{c,\rm PPT}(\rho_{AB})$ , with the latter fact proved through a new lower bound on the entanglement cost.
The work [8] established a general no-go result for entanglement reversibility: it showed that entanglement manipulation remains irreversible under any class of operations which are non-entangling (NE), in the sense that 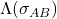$\Lambda(\sigma_{AB})$ is separable for any separable 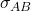$\sigma_{AB}$ . This effectively prohibits a reversible theory of entanglement without generating more entanglement in the process. The result relies on the introduction of a stronger lower bound on entanglement cost, which then leads to the strict inequality 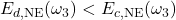$E_{d,\rm NE}(\omega_3) < E_{c,\rm NE}(\omega_3)$ for a specific maximally correlated two-qutrit state $\omega_3$ .

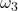Conjectured solution

In [9] it was claimed that there exists a class of operations — asymptotically non-entangling maps — for which entangled states can indeed be reversibly interconverted. Specifically, define the global (generalised) robustness of entanglement as

$R_g(\rho) := \inf \left\{ \lambda \,\left|\; \frac{\rho + \lambda \omega}{1+\lambda} \text{ separable}, \; \omega \text{ any state} \right.\right\}.$

The class of $(R_g, \delta)$ -approximately non-entangling operations is then defined as those channels $\Lambda$ such that $R_g(\Lambda(\sigma)) \leq \delta$ for any separable $\sigma$ . [9] then studied asymptotic transformation rates of the form

$\displaystyle r_{{\rm NE}, R_g} (\rho \to \omega) = \sup \left\{ r \,\left|\; \lim_{n \to \infty} \inf_{\Lambda_n \in (R_g, \delta_n)-{\rm NE}} \left\| \Lambda_n\left(\rho_{AB}^{\otimes n}\right) - \sigma_{A'B'}^{\otimes \floor{rn}} \right\|_1 = 0,\; \lim_{n\to\infty} \delta_n = 0 \right.\right\},$

that is, where entanglement generation is explicitly allowed, but the generated entanglement $\delta_n$ (as quantified by $R_g$ ) has to vanish in the asymptotic limit. The main claim of [9] was that $E_{d,{\rm NE}, R_g} (\rho_{AB}) = E_{c,{\rm NE},R_g}(\rho_{AB}) = E^\infty_R(\rho_{AB})$ holds for any quantum state. Together with the result of [8], this would complete the solution of Problem 20: we would have that asymptotically non-entangling operations form a reversible theory of entanglement, and it is effectively the smallest class of operations for which this is possible, as we know that some entanglement generation is necessary for reversibility.

However, in [10] an issue was discovered in the proof of the main result of [9], bringing the reversibility claim into question. The complete solution of Problem 20 thus remains an open problem.

Of note is the fact that the choice of $R_g$ in the conjectured solution of [9] appears to be crucial. This is because [8] showed that even a small change of the measure with respect to which entanglement is quantified, from the global robustness $R_g$ to the standard (separable) robustness

$R_s(\rho) := \inf \left\{ \lambda \,\left|\; \frac{\rho + \lambda \omega}{1+\lambda} \text{ separable}, \; \omega \text{ separable} \right.\right\}$

makes the theory irreversible: $E_{d,{\rm NE}, R_s}} (\omega_3) < E_{c,{\rm NE},R_s}(\omega_3)$ . Put another way, any attempt to establish a reversible theory of entanglement must allow exponentially large amounts of entanglement to be generated with respect to $R_s$ , although the entanglement may asymptotically vanish according to other measures such as $R_g$ .

References

[1] C.H. Bennett, H.J. Bernstein, S. Popescu and B. Schumacher, Concentrating partial entanglement by local operations, Phys. Rev. A 53, 2046 (1996) and quant-ph/9511030 (1995).

[2] G. Vidal and J.I. Cirac, Irreversibility in asymptotic manipulations of entanglement, Phys. Rev. Lett. 86, 5803 (2002) and quant-ph/0102036 (2001).

[3] M. Horodecki, A. Sen, and U. Sen, Rates of asymptotic entanglement transformations for bipartite mixed states: maximally entangled states are not special, Phys. Rev. A 67, 062314 (2003) and quant-ph/0207031 (2002).

[4] E.M. Rains, A semidefinite program for distillable entanglement, IEEE T. Inform. Theory 47, 2921 (2001) and quant-ph/0008047 (2000).

[5] K. Audenaert, M.B. Plenio and J. Eisert, Entanglement cost under positive-partial-transpose-preserving operations, Phys. Rev. Lett. 90, 027901 (2003).

[6] S. Ishizaka and M. B. Plenio, Multiparticle entanglement under asymptotic positive-partial-transpose-preserving operations, Phys. Rev. A 72, 042325 (2005) and quant-ph/0503025 (2005).

[7] X. Wang and R. Duan, Irreversibility of Asymptotic Entanglement Manipulation Under Quantum Operations Completely Preserving Positivity of Partial Transpose, Phys. Rev. Lett. 119, 180506 (2017).

[8] L. Lami and B. Regula, No second law of entanglement manipulation after all, Nat. Phys. 19, 184–189 (2023) and arXiv:2111.02438 (2021).

[9] F. Brandão and M. B. Plenio, A Reversible Theory of Entanglement and its Relation to the Second Law, Commun. Math. Phys. 295, 3 (2010) and arXiv:0710.5827 (2007).

[10] M. Berta, F. Brandão, G. Gour, L. Lami, M. B. Plenio, B. Regula, and M. Tomamichel, On a gap in the proof of the generalised quantum Stein’s lemma and its consequences for the reversibility of quantum resources, arXiv:2205.02813 (2022).