The entanglement cost of f-routing – Open Quantum Problems

Cite this problem as Problem 48.

Problem

$f$ -routing is a distributed task involving two players, Alice and Bob, who co-operate to redirect a quantum system $Q$ based on the value of classical inputs $x,y$ . Given a Boolean function $f:\{0,1\}^n\times \{0,1\}^n\to\{0,1\}$ , an $f$ -routing protocol has the following communication pattern:

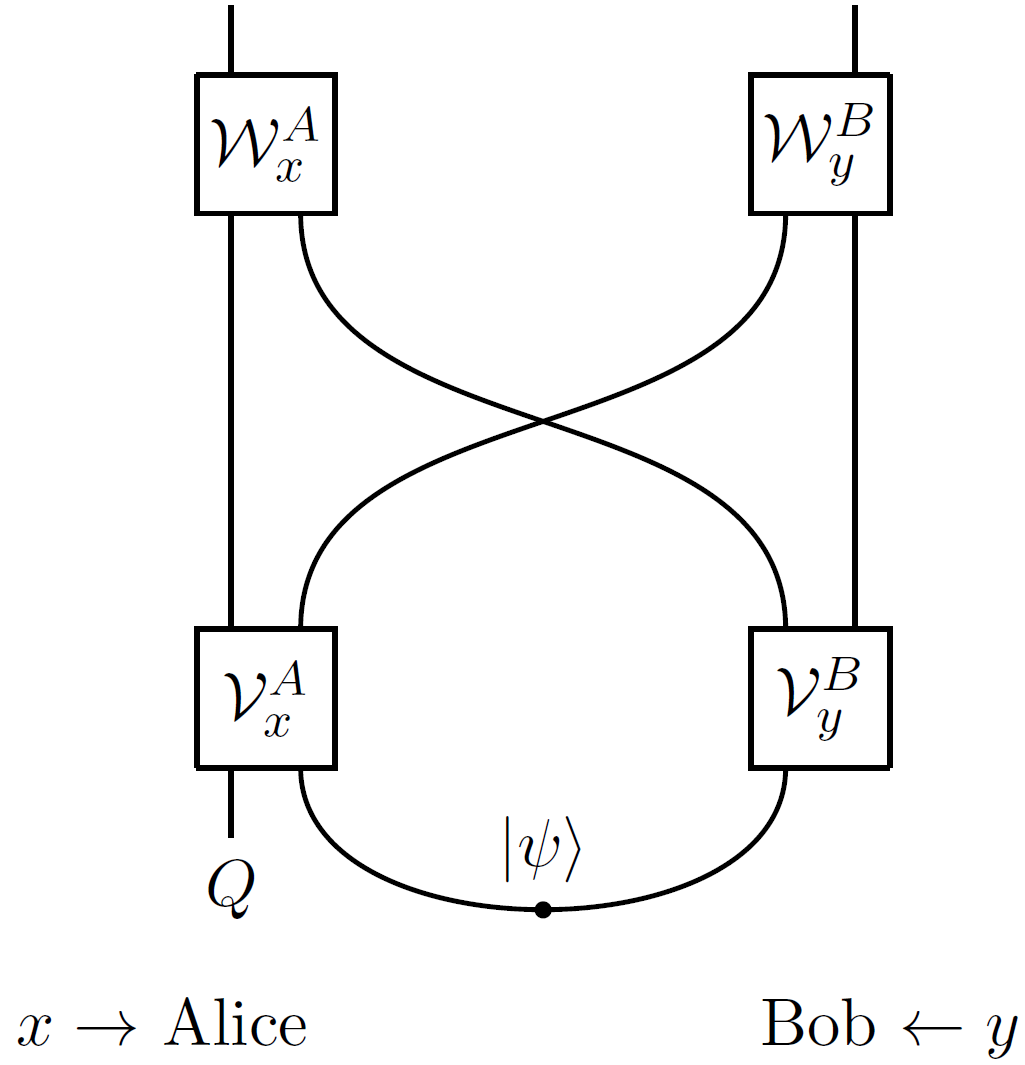
The diagram should be read from bottom to top. The lower curved wire represents an initial shared entangled state $|\psi\rangle$ held between Alice and Bob: the logarithm of its local dimension is the entanglement cost of the protocol. After receiving input $x\in\{0,1\}^n$ , Alice performs the quantum operation ${\cal V}_x^A$ on both system $Q$ and her part of the shared entangled state. This operation outputs two quantum systems, one of which she sends to Bob. Similarly, upon receiving input $y\in\{0,1\}^n$ , Bob implements the quantum operation ${\cal V}_y^B$ on his part of the state, which also outputs two quantum systems, one of which he sends to Alice. Alice then implements the operation ${\cal W}_x^A$ on her remaining quantum system and the quantum system she receives from Bob; similarly, Bob implements the operation ${\cal W}_y^B$ on his remaining quantum system and the system he receives from Alice.

Let ${\cal I}$ denote the identity channel on system $Q$ , and let $\Omega^A_{xy}$ ( $\Omega^B_{xy}$ ) denote the induced quantum channel from $Q$ to Alice’s (Bob’s) final system. The $f$ -routing protocol is correct if, for all $x,y$ with $f(x,y)=0$ , it holds that $\Omega^A_{xy}={\cal I}$ ; and, for all $x,y$ with $f(x,y)=1$ , it holds that $\Omega^B_{xy}={\cal I}$ . At the end of a correct $f$ -routing protocol, the initial quantum state of system $Q$ will hence end up at Alice’s or Bob’s lab depending on the value of $f(x,y)$ .

For $\epsilon>0$ , the $f$ -routing protocol is $\epsilon$ -sound if

$\|\Omega_{xy}^A-{\cal I}\|_\diamond\leq \epsilon,\mbox{ for } x,y, \mbox{ with }f(x,y)=0,$

$\|\Omega_{xy}^B-{\cal I}\|_\diamond\leq \epsilon,\mbox{ for } x,y, \mbox{ with }f(x,y)=1,$

where $\|\|_\diamond$ denotes the diamond norm.

Question: For fixed $\epsilon>0$ , find a sequence of explicit Boolean functions $(f_n)_n$ , with $f_n:\{0,1\}^{n}\times\{0,1\}^{n}\rightarrow \{0,1\}$ , for which the minimum entanglement cost of an $\epsilon$ -sound $f$ -routing protocol scales as $\mbox{poly}(n)$ .

Background

The $f$ -routing task was introduced in the quantum position-verification setting [1, 2]. In that context, proving an entanglement lower bound on $f$ -routing establishes the security of a quantum position-verification scheme. This scheme has the property that an honest player performs nearly only classical operations: they compute $f(x,y)$ and then redirect $Q$ based on the outcome. Meanwhile, it is hoped that the dishonest player (who uses the non-local quantum computation model) needs entanglement that grows with $n$ , preferably polynomially. It was also shown that several other proposals for quantum position-verification are equivalent to $f$ -routing, in the sense that entanglement cost across all these settings are all related polynomially. Thus, good $f$ -routing lower bounds are a necessary step to establishing the security of many QPV schemes.

In [3], it was observed that $f$ -routing is closely related to the \emph{conditional disclosure of secrets} primitive studied in information-theoretic classical cryptography. In particular, it was shown that the randomness cost in CDS for a function $f$ , call it $CDS(f)$ , upper bounds the entanglement cost in $f$ -routing for the same function, $E(f)$ ,

$CDS(f) \geq E(f).$

Thus, poly $(n)$ lower bounds on entanglement in $f$ -routing would imply poly $(n)$ lower bounds on randomness in CDS. Obtaining such CDS lower bounds has been identified as an important open problem in classical cryptography [4].

$CDS(f)$ is also known to be upper bounded by the size of a secret sharing scheme with indicator function $f$ , and by the size of a span program computing $f$ [5]. Hence, $f$ -routing lower bounds also lower bound these settings.

Partial Results

The work of [6] proved linear lower bounds on ancilla size for random functions. There are also some restrictions on the model, which takes Alice and Bob’s actions to be unitary.

In [7], linear lower bounds on entanglement for several explicit functions in the case where the $f$ -protocol is perfect in either $f=0$ or $f=1$ instances are derived. The technique is based on the non-deterministic rank of the specified function.

For CDS, logarithmic lower bounds are proven in [8]. These were adapted to quantum CDS in [9].

References

[1] A. Kent, W. J. Munro, and T. P. Spiller, Physical Review A, 84(1):012326 (2011).
[2] H. Buhrman, S. Fehr, C. Schaffner, and F. Speelman. The garden-hose model. In Proceedings of the 4th conference on Innovations in Theoretical Computer Science, pages 145–158, (2013).
[3] R. Allerstorfer, H. Buhrman, A. May, F. Speelman and P. V. Lunel, Quantum, 8:1387, (2024).
[4] Benny Applebaum and Prashant Nalini Vasudevan. Placing conditional disclosure of secrets in the communication complexity universe. Journal of Cryptology, 34(2):11, (2021).
[5] Y. Gertner, Y. Ishai, E. Kushilevitz, and T. Malkin. Protecting data privacy in private information retrieval schemes. In Proceedings of the thirtieth annual ACM symposium on Theory of computing, pages 151–160, (1998).
[6] A. Bluhm, S. Höfer, A. May, M. Stasiuk, P. V. Lunel, and H. Yuen, arXiv preprint arXiv:2505.23893.
[7] V. R Asadi, E. Culf, and A. May, arXiv preprint arXiv:2402.18647.
[8] R. Gay, I. Kerenidis, and H. Wee. Communication complexity of conditional disclosure of secrets and attribute-based encryption. In Annual Cryptology Conference, pages 485–502. Springer (2015).
[9] V. R. Asadi, K. Kuroiwa, D. Leung, A. May, S. Pasterski, and C. Waddell, Quantum, 9:1885 (2025).