Cite this problem as Problem 29.
Problem
Entanglement of formation is defined as a minimum over all convex decompositions of a bipartite state into pure states (see Problem 7). It has been shown that for certain two-mode Gaussian states this minimum can be taken over decompositions of the given state into pure states, all of which are translates of the same squeezed Gaussian state with Gaussian weights. Show (or disprove) that this is true for all Gaussian states.
Background
For a generic (mixed) bipartite quantum state ![]() , the entanglement of formation is defined by
, the entanglement of formation is defined by
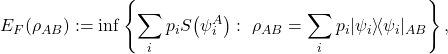
where the infimum runs over all decompositions ![]() of
of ![]() as a convex combination of pure states,
as a convex combination of pure states, ![]() is the reduced state of
is the reduced state of ![]() on the A system, and
on the A system, and ![]() is the von Neumann entropy. If the system AB is finite dimensional, the above decompositions can be taken to have a finite number of pure states, at most equal to
is the von Neumann entropy. If the system AB is finite dimensional, the above decompositions can be taken to have a finite number of pure states, at most equal to ![]() [1]. If AB is infinite dimensional, instead, one could replace the discrete sum with a more general integral over a Borel measure with barycenter
[1]. If AB is infinite dimensional, instead, one could replace the discrete sum with a more general integral over a Borel measure with barycenter ![]() on the space of pure states [2, Section 8]. By doing so, one obtains in principle a different entanglement measure, which is in many ways a better generalisation of the entanglement of formation. Fortunately, however, the two versions of the entanglement of formation (with finite vs integral decompositions) coincide whenever either of the local entropies is finite [2, Section 8]. Remarkably, this is the case for all Gaussian states, so for the sake of this problem one can replace the above discrete decompositions with integrals without affecting the definition.
on the space of pure states [2, Section 8]. By doing so, one obtains in principle a different entanglement measure, which is in many ways a better generalisation of the entanglement of formation. Fortunately, however, the two versions of the entanglement of formation (with finite vs integral decompositions) coincide whenever either of the local entropies is finite [2, Section 8]. Remarkably, this is the case for all Gaussian states, so for the sake of this problem one can replace the above discrete decompositions with integrals without affecting the definition.
When the state ![]() is Gaussian, one can consider a further measure called the Gaussian entanglement of formation [3], obtained by requiring that all states
is Gaussian, one can consider a further measure called the Gaussian entanglement of formation [3], obtained by requiring that all states ![]() appearing in the decomposition of
appearing in the decomposition of ![]() be Gaussian pure states. In [3] it is also shown that if the initial bipartite state is Gaussian and all pure states in the decomposition are also assumed to be Gaussian, then also the probability distribution associated with the decomposition can be taken to be Gaussian without loss of generality. This follows from [3, Proposition 1], once one observes that adding a positive semidefinite matrix to the covariance matrix of any Gaussian state can always be accomplished with Gaussian noise.
be Gaussian pure states. In [3] it is also shown that if the initial bipartite state is Gaussian and all pure states in the decomposition are also assumed to be Gaussian, then also the probability distribution associated with the decomposition can be taken to be Gaussian without loss of generality. This follows from [3, Proposition 1], once one observes that adding a positive semidefinite matrix to the covariance matrix of any Gaussian state can always be accomplished with Gaussian noise.
With this, the above question reads: Does the entanglement of formation equal the Gaussian entanglement of formation for all Gaussian states?
Answering this in the affirmative would have tangible implications for concrete computations. Indeed, the Gaussian entanglement of formation of a Gaussian state can be computed more easily than the general entanglement of formation, by solving an optimisation over covariance matrices [3, Proposition 1] instead of infinite-dimensional ensembles. A full solution needs to consider the multi-mode case as well, as it is known that in order to obtain the operationally meaningful entanglement cost one needs to regularise the entanglement of formation (Problems 7 and 10) [4].
Partial Results
- It has been shown in [5] that the Gaussian entanglement of formation equals the entanglement of formation for two-mode Gaussian states which are symmetric with respect to interchange of the modes.
- In [7] the assumption of symmetry has been removed, thus proving the conjecture for all two-mode Gaussian states. The argument in [7] relies on a generalisation of the approach of [5] and on the proof of the conjecture in [6]. A full solution of the two-mode case was claimed before in [8], but in [7, p. 4194] it is observed that the proof in [8] is incomplete.
References
[1] A. Uhlmann, Entropy and optimal decompositions of states relative to a maximal commutative subalgebra, Open Syst. Inf. Dyn. 5, 209-228 (1998) and arXiv:quant-ph/9704017 (1997).
[2] M. E. Shirokov, On properties of quantum channels related to their classical capacity, Theory Probab. Its Appl. 52, 250-276 (2008).
[3] M. Wolf, G. Giedke, O. Krüger, R. F. Werner, and J. I. Cirac, Gaussian entanglement of formation, Phys. Rev. A 69, 052320 (2004) and arXiv:quant-ph/0306177 (2003).
[4] P. M. Hayden, M. Horodecki, and B. M. Terhal, The asymptotic entanglement cost of preparing a quantum state, J. Phys. A 34, 6891-6898 (2001) and arXiv:quant-ph/0008134 (2000).
[5] G. Giedke, M. M. Wolf, O. Krüger, R. F. Werner, and J. I. Cirac, Entanglement of formation for symmetric Gaussian states, Phys. Rev. Lett. 91, 107901 (2003) and arXiv:quant-ph/0304042 (2003).
[6] J. Solomon Ivan and R. Simon, Entanglement of formation for Gaussian states, Preprint arXiv:0808.1658 (2008).
[7] Y. Akbari-Kourbolagh and H. Alijanzadeh-Boura, On the entanglement of formation of two-mode Gaussian states: a compact form, Quantum Inf. Process. 14, 4179-4199 (2015) and arXiv:1402.3321 (2014).
[8] P. Marian and T. A. Marian, Entanglement of formation for an arbitrary two-mode Gaussian state, Phys. Rev. Lett. 101, 220403 (2008) and arXiv:0809.0321 (2008).