Cite this problem as Problem 36.
Problem
Consider a physical system where a number of (possibly incompatible) experiments can be in principle conducted. Each experiment ![]() allows estimating a property with value
allows estimating a property with value ![]() , and any vector of possible values
, and any vector of possible values ![]() , with
, with ![]() is called a history. The above is called a joint measurement framework [1].
is called a history. The above is called a joint measurement framework [1].
Given the set of all histories ![]() , define a Hilbert space
, define a Hilbert space ![]() by assigning to each
by assigning to each ![]() an element
an element ![]() of an orthonormal basis
of an orthonormal basis ![]() . For any
. For any ![]() , define the vector
, define the vector ![]() . To model experiments on this system within the framework of Sorkin’s quantum measure theory [2], we assume that there exists a complex-valued operator
. To model experiments on this system within the framework of Sorkin’s quantum measure theory [2], we assume that there exists a complex-valued operator ![]() , dubbed decoherence functional, with the following properties:
, dubbed decoherence functional, with the following properties:
- Hermiticity:
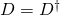 .
. - Weak positivity:
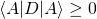 , for all
, for all 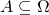 .
. - Normalization:
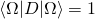 .
. - Strong decoherence: let
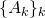 be a partition of
be a partition of 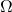 . If there exists a feasible experiment to determine which
. If there exists a feasible experiment to determine which 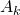 describes the system, then
describes the system, then 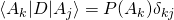 , where
, where 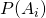 is the probability that the history of the system belongs to
is the probability that the history of the system belongs to 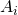 .
.
Note that, given that there exist experimental setups to measure the basic properties ![]() , for any
, for any ![]() , the partition of
, the partition of ![]()
![]() , with
, with
![]()
is measurable and by axiom ![]() thus satisfies
thus satisfies ![]() , where
, where ![]() is the probability to obtain the result
is the probability to obtain the result ![]() had we decided to conduct experiment
had we decided to conduct experiment ![]() .
.
To describe two or more independent systems, with history sets ![]() , we consider the set of joint histories
, we consider the set of joint histories ![]() and take the decoherence functional
and take the decoherence functional ![]() describing the joint system as
describing the joint system as ![]() . It is observed in [3], though, that the tensor product of two valid decoherence functionals may not satisfy the axiom of weak positivity. That is, even when
. It is observed in [3], though, that the tensor product of two valid decoherence functionals may not satisfy the axiom of weak positivity. That is, even when ![]() satisfy all the axioms above, there may be a vector
satisfy all the axioms above, there may be a vector ![]() such that
such that ![]() . As noted in [3], this is not the case when, instead of weak positivity, we demand the stronger axiom of strong positivity, i.e., the requirement that, when viewed as a matrix,
. As noted in [3], this is not the case when, instead of weak positivity, we demand the stronger axiom of strong positivity, i.e., the requirement that, when viewed as a matrix, ![]() is positive semidefinite (
is positive semidefinite (![]() ). In fact, the set of strongly positive decoherence functionals is closed under tensor products.
). In fact, the set of strongly positive decoherence functionals is closed under tensor products.
Problem: identify a set of decoherence functionals that is closed under tensor products and that contains elements which are not strongly positive. Equivalently, find a joint measure framework and a decoherence functional ![]() describing it such that
describing it such that ![]() and, for all
and, for all ![]() ,
, ![]() satisfies the axiom of weak positivity.
satisfies the axiom of weak positivity.
Background
The problem of reconciling quantum theory with general relativity is as old as quantum mechanics itself. One approach to achieve this unification, pioneered by Sorkin [2] and independently by Hartle [4], begins with a reformulation of quantum theory in terms of histories, rather than instantaneous states. It is within this approach that Sorkin proposed his history-based framework of quantum measure theory, which can accommodate, not only classical and quantum mechanics, but also some physical theories beyond the quantum formalism. In [1], [3] it is raised the problem of which set of decoherence functionals to consider, and the strongly positive set is argued on the basis of composability. By adopting strong positivity as a fundamental axiom, though, we may be limiting unnecessarily the space of possible physical theories which quantum measure theory can handle.
Partial results
In [5] it is proven that, for any ![]() , there exists a joint measurement scenario and a decoherence functional
, there exists a joint measurement scenario and a decoherence functional ![]() describing it such that
describing it such that ![]() satisfies weak positivity, but
satisfies weak positivity, but ![]() does not. It is also shown that the set of strongly positive decoherence functionals cannot be enlarged without losing the property of being closed under under tensor products. In fact, in [5] the authors identify a family
does not. It is also shown that the set of strongly positive decoherence functionals cannot be enlarged without losing the property of being closed under under tensor products. In fact, in [5] the authors identify a family ![]() of quantum decoherence functionals with the property that any set of decoherence functionals closed under tensor products that contains
of quantum decoherence functionals with the property that any set of decoherence functionals closed under tensor products that contains ![]() can only contain strongly positive elements.
can only contain strongly positive elements.
References
[1] F. Dowker, J. Henson and P. Wallden, New J. Phys. 16, 033033 (2014).
[2] R. D. Sorkin, Quantum Mechanics as Quantum Measure Theory, Mod. Phys. Lett. A9 3119-3128 (1994).
[3] X. Martin, D. OConnor and R.D. Sorkin, Random walk in generalized quantum theory, Phys. Rev. D 71, 024029 (2005).
[4] J. B. Hartle, The quantum mechanics of cosmology Dec 1989, Lectures at Winter School on Quantum Cosmology and Baby Universes, Jerusalem, Israel, Dec 27, 1989 – Jan 4, 1990.
[5] P. Boes and M. Navascues, Phys. Rev. A 95, 022114 (2017).