Cite this problem as Problem 4.
Problem
By a theorem of Nielsen [1], we have a completely explicit criterion to decide when a single copy of a pure bipartite state can be converted to another such state using only local quantum operations and classical communication. Using Nielsen’s criterion, one can show the existence of the phenomenon of catalysis [2]: there exist situations when a state ![]() cannot be converted to state
cannot be converted to state ![]() , but nevertheless
, but nevertheless ![]() can be converted to
can be converted to ![]() for a suitably chosen entangled state
for a suitably chosen entangled state ![]() , the “catalyst”.
, the “catalyst”.
The problem is to give a similarly efficient criterion to decide which pure bipartite states can be converted into each other using a catalyst.
Background
Nielsen’s criterion provides a surprisingly direct rendering of the intuition that a “more entangled” pure state has a “more mixed” reduced state. Thus a bipartite pure state ![]() can be converted to
can be converted to ![]() if and only if the eigenvalue vector of the partial trace of
if and only if the eigenvalue vector of the partial trace of ![]() is more mixed than that of
is more mixed than that of ![]() , in the sense of majorisation of probability vectors [3]. We say that one probability vector
, in the sense of majorisation of probability vectors [3]. We say that one probability vector ![]() is majorised by another,
is majorised by another, ![]() , if one and hence all of the following equivalent statements hold:
, if one and hence all of the following equivalent statements hold:
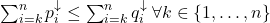 , where
, where 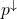 and
and 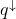 denotes the vectors brought into non-increasing order.
denotes the vectors brought into non-increasing order.- There is a doubly stochastic matrix
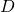 (positive entries, sum of all rows and all columns = 1) such that
(positive entries, sum of all rows and all columns = 1) such that 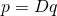 .
. - For every convex function
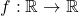 , we have
, we have 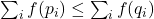 .
.
Denoting the above condition as ![]() , we have that
, we have that ![]() can be converted to
can be converted to ![]() with LOCC if and only if
with LOCC if and only if ![]() [1], where
[1], where ![]() denotes the vector of eigenvalues of a given operator.
denotes the vector of eigenvalues of a given operator.
The problem of existence of catalysts for such a transformation can be rephrased completely in this context of majorisation of classical probability vectors, since tensoring pure bipartite states means again tensoring of probability vectors for the eigenvalues of the reduced density operators. Thus we would like to characterize the order relation of “catalytic majorisation”:
- When does there exist a vector
 such that
such that 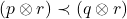 ?
?
Solution
A complete solution was independently obtained by Klimesh [3, 4] and Turgut [5]. It can be phrased in terms of classical Rényi entropies, which are defined as
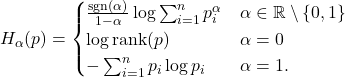
We additionally need the function ![]()
The main finding of [4] and [5] is then as follows. Consider vectors ![]() such that
such that ![]() and at least one of
and at least one of ![]() and
and ![]() has no zero components. Then, the following are equivalent:
has no zero components. Then, the following are equivalent:
- There exists a vector
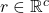 such that
such that 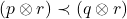 .
. 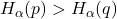 for all
for all 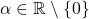 and
and 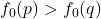 .
.
The condition can be simplified if one only requires that the transformation from ![]() to
to ![]() be realised approximately. In [6] it was then shown that, for all vectors
be realised approximately. In [6] it was then shown that, for all vectors ![]() such that
such that ![]() , the following are equivalent:
, the following are equivalent:
- For any
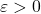 , there exists a vector
, there exists a vector 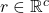 such that
such that 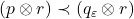 for some
for some 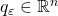 with
with 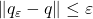 .
. 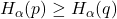 for all
for all 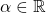 .
.
Note that the dimension of the catalyst, ![]() in the above, is generally unbounded [7].
in the above, is generally unbounded [7].
One should also note that an alternative condition for catalytic transformations that only uses Rényi entropies with ![]() was independently established in [8].
was independently established in [8].
References
[1] M. A. Nielsen, Phys. Rev. Lett. 83, 436-439 (1999), quant-ph/9811053.
[2] D. Jonathan and M. B. Plenio, Phys. Rev. Lett. 83, 3566-3569 (1999), quant-ph/9905071.
[3] M. Klimesh, Entropy Measures and Catalysis of Bipartite Quantum State Transformations, Proc. 2004 International Symposium on Information Theory (ISIT 2004), June 27-July 2, 2004, Page 357.
[4] M. Klimesh, Inequalities that Collectively Completely Characterize the Catalytic Majorization Relation, quant-ph/0709.3680.
[5] S. Turgut, Necessary and Sufficient Conditions for the Trumping Relation, J. Phys. A: Math. Theor. 40 (2007) 12185-12212.
[6] F. Brandao, M. Horodecki, N. H. Y. Ng, J. Oppenheim, and S. Wehner, The second laws of quantum thermodynamics, PNAS 112, 3275 (2015).
[7] S. Daftuar and M. Klimesh, Mathematical structure of entanglement catalysis, Phys. Rev. A 64, 042314 (2001).
[8] G. Aubrun and I. Nechita, Catalytic Majorization and ℓp Norms, Commun. Math. Phys. 278, 133-144 (2008).